The Perfect Square Of 25: Unveiling The Essence Of A Mathematical Concept

The Perfect Square of 25: Unveiling the Essence of a Mathematical Concept

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Perfect Square of 25: Unveiling the Essence of a Mathematical Concept. Let’s weave interesting information and offer fresh perspectives to the readers.

Video about The Perfect Square of 25: Unveiling the Essence of a Mathematical Concept

The Perfect Square of 25: Unveiling the Essence of a Mathematical Concept

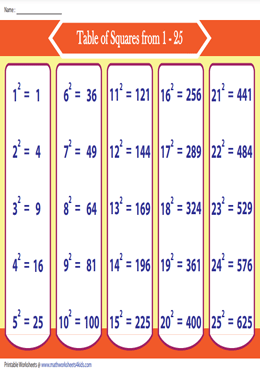
What is the Square of 25?" - Unveiling the Mystery of Numbers

In the realm of mathematics, the concept of a perfect square holds immense significance. A perfect square is a positive integer that can be expressed as the square of another integer. Among the myriad of perfect squares, the square of 25, denoted as 25², stands out as a fundamental building block in mathematical operations.

Delving into the Concept of a Perfect Square

A perfect square can be visualized as a square with equal sides. The length of each side corresponds to the square root of the perfect square. For instance, the perfect square of 4 is 16, and the square root of 16 is 4. This relationship between a perfect square and its square root is a cornerstone of mathematical operations.

Unveiling the Perfect Square of 25: 25²

The perfect square of 25 is a particularly important concept due to its prevalence in mathematical calculations. 25² can be calculated by multiplying 25 by itself:

25² = 25 × 25 = 625

Therefore, the perfect square of 25 is 625.

Exploring the Properties of 625

As the perfect square of 25, 625 possesses several noteworthy properties:

  • Divisibility: 625 is divisible by 1, 5, 25, 125, and 625.
  • Prime Factorization: The prime factorization of 625 is 5³.
  • Square Root: The square root of 625 is 25, as 25² = 625.
  • Oddity/Evenness: 625 is an odd number.

Applications of the Perfect Square of 25 in Mathematics

The perfect square of 25 finds applications in various mathematical operations and concepts:

  • Algebra: 625 is used in algebraic equations and polynomials.
  • Geometry: 625 represents the area of a square with sides of length 25 units.
  • Number Theory: 625 is a factor of the Fibonacci number F₁₅.
  • Calculus: 625 appears in derivatives and integrals of certain functions.

The Significance of Perfect Squares in Mathematics and Beyond

Perfect squares, including the perfect square of 25, play a vital role in mathematics due to their:

  • Simplicity: They are easily calculated and understood.
  • Foundation: They form the basis for many mathematical operations.
  • Applications: They are applied in various fields, including geometry, algebra, and number theory.

Beyond mathematics, perfect squares have practical applications in:

  • Architecture: Designing symmetrical and aesthetically pleasing structures.
  • Engineering: Calculating forces and stresses in structures.
  • Computer Science: Developing efficient algorithms and data structures.

Conclusion

The perfect square of 25, represented as 625, is a fundamental concept in mathematics with a wide range of applications. Its simplicity, foundation, and versatility make it an essential tool in mathematical operations and beyond. Understanding the concept of a perfect square and the significance of 625 provides a deeper appreciation for the beauty and power of mathematics.

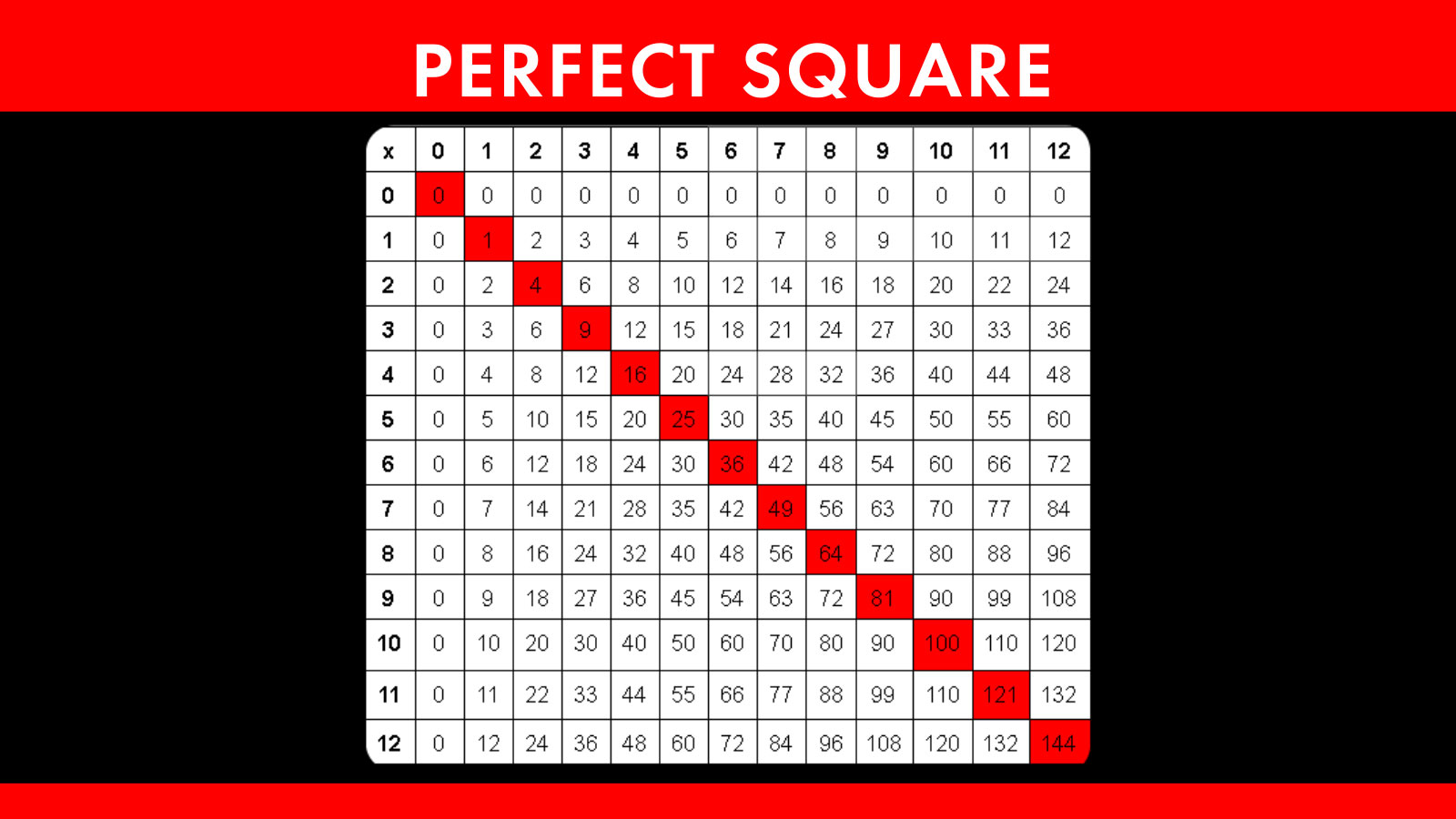
What is the Square of 25?" - Unveiling the Mystery of Numbers HowStuffWorks - Learn How Everything Works! SOLVED:Factor the perfect squares. 25 x^2+10 x+1
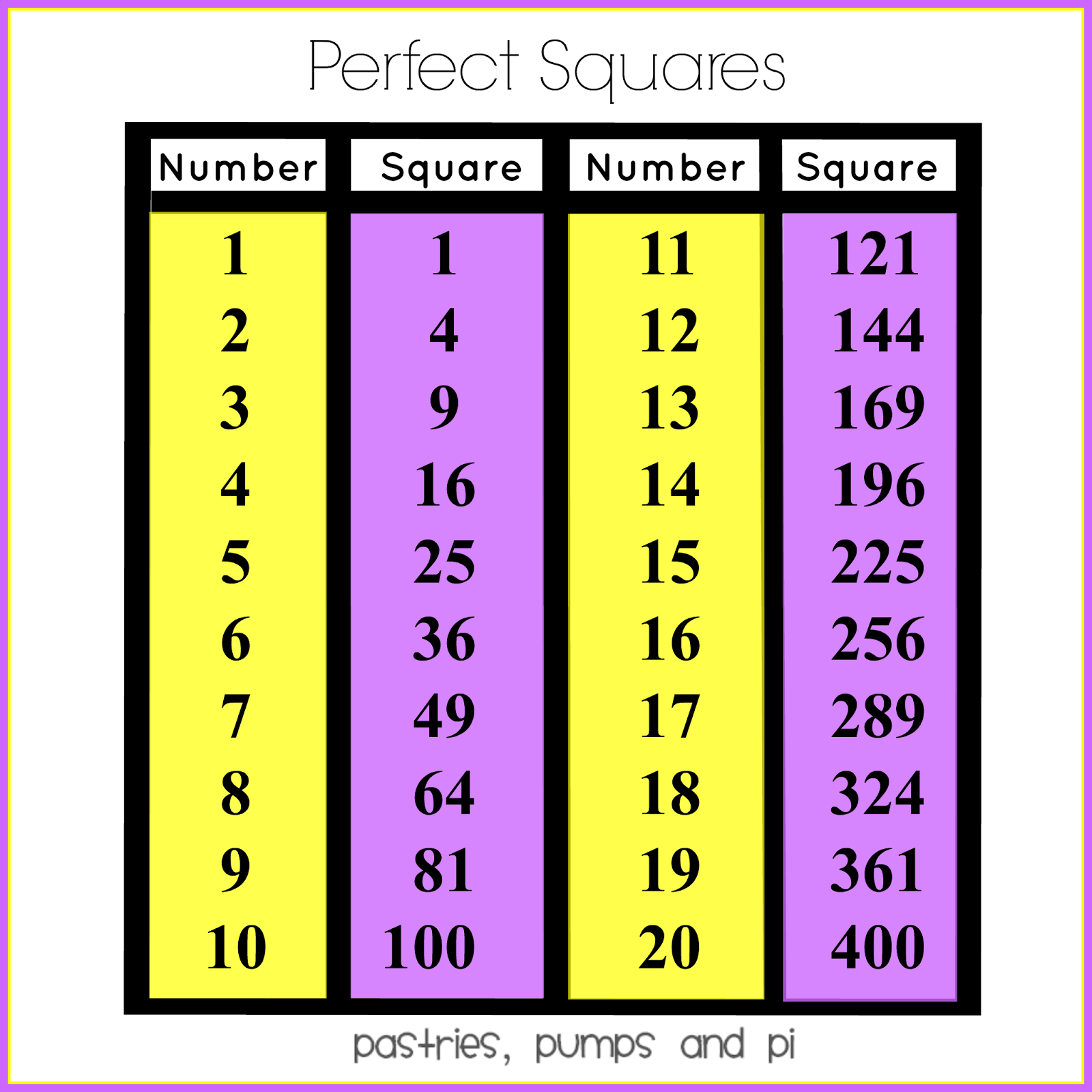
FREEBIE: Perfect Square Chart Poster and Student Reference Sheet for students Free math Chart Of Perfect Squares And Cubes Perfect Square Trinomials
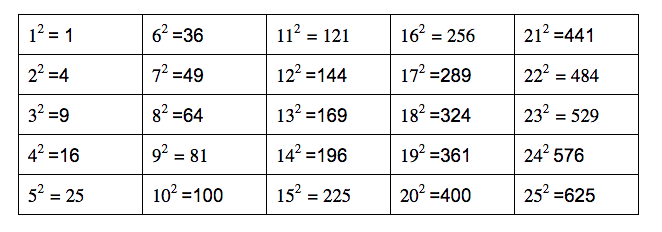
Perfert Squares-Cubes-Fourths-1 to 25 MooMooMath and Science TIP BELAJAR MATEMATIK (TIPS FOR LEARNING MATHEMATICS): PERFECT SQUARES

Closure

Thus, we hope this article has provided valuable insights into The Perfect Square of 25: Unveiling the Essence of a Mathematical Concept. We appreciate your attention to our article. See you in our next article!

By